PID kontrolieri tiek izmantoti, lai ietekmētu noteiktus mērāmos lielumus. Kā gudri 3-in-1 kontrolieri tie katru dienu sevi pierāda daudzās rūpnieciskās sistēmās un ļoti precīzi kontrolē līdz pat iestatītajai vērtībai. Mēs piedāvājam jums svarīgākos faktus un skaitļus par PID regulēšanu.
Kompaktu kontrolieri var pielāgot visdažādākajiem lietojumiem, un parasti to izmanto kā PID kontrolieri. Tas darbojas proporcionāli, integrējoši un diferencējoši (PID). Šajā gadījumā atsevišķu komponentu intensitāte tiek pielāgota vadības procesam. Tas tiek panākts, nosakot kontroles parametru dimensiju.
PID regulatora darbības princips ir salīdzinoši vienkārši izskaidrojams. Neatkarīgi no tā, vai tas ir PID temperatūras regulators vai PID mitruma regulators, regulators vienmēr mēģina pielāgot konkrēto regulējamo mainīgo lielumu iestatītajai vērtībai, pamatojoties uz faktisko vērtību. Šajā gadījumā P komponente pastiprina vadības novirzi, I komponente palielina izejas līmeni esošās vadības novirzes gadījumā, bet D komponente neitralizē faktiskās vērtības kustību. Komponentus, kas nav nepieciešami kontrolei, var deaktivizēt. Atkarībā no pielietojuma tie tad darbojas kā PI kontrolieri, P kontrolieri, PD kontrolieri vai I kontrolieri.
PID struktūra nodrošina vislabāko vadības reakciju lielākajā daļā lietojumu. Tāpēc PID kompaktie kontrolieri ir ļoti izplatīti temperatūras regulēšanas jomā. Tie ļauj arī tieši pieslēgt RTD temperatūras zondes un termopārus. Dažiem kontrolējamiem mainīgajiem lielumiem, tostarp ātrumam un plūsmai, nepieciešams atslēgt atsevišķus komponentus.
P komponente reaģē ļoti ātri un pastiprina vadības starpību; tās pastāvīgajai vadības novirzei ir nelabvēlīga ietekme. Atbildīgais vadības parametrs ir proporcionālā josla Pb. Ar mazāku Pb regulators kļūst ātrāks un vadības novirze mazāka. Tomēr visai sistēmai kopumā ir tendence arvien vairāk svārstīties.
I komponents novērš vadības novirzi. Ja atiestatīšanas laiks rt tiek iestatīts mazāks, regulators ātrāk izveido izejas līmeni un arī ātrāk neitralizē vadības novirzi. Tomēr, ja iestatījums ir pārāk mazs, rodas arī svārstības.
D komponente neitralizē faktiskās vērtības kustību. Tas nozīmē, ka sildīšanas regulatoram šī komponente tiek samazināta, kad faktiskā vērtība palielinās, un palielināta, kad faktiskā vērtība samazinās. Aprakstītajai uzvedībai ir slāpējošs efekts. Atbildīgais parametrs ir atvasinājuma laiks dt. Jo lielāks dt ir iestatīts, jo lielāks ir aprakstītais efekts.
Vadības procesa uzvedība vienmēr ir atkarīga no darba punkta. Tāpēc pirms regulēšanas iekārta jāiestata tādā darba stāvoklī, kuram vēlāk ir sagaidāmi labvēlīgi vadības parametri. Piemēram, pirms regulēšanas ir jānoslogo krāsns vai jārada pieprasījums plūsmas sildītājam. Ja iestatīšanas laikā jānorāda iestatītā vērtība, tai jāatrodas turpmākajā darba diapazonā.
Ja pastāv salīdzināmas iekārtas/kontroles cilpas, tajās izmantotos kontroles parametrus var izmantot izmēģinājuma režīmā. Ja šāda pieeja nenoved pie mērķa, var izmantot kādu no turpmāk minētajām optimizācijas metodēm.
Svārstību metode saskaņā ar Zīgleru un Nikolsu
Šo metodi izmanto salīdzinoši ātri kontrolējamām sistēmām. Lai sagatavotos, tiek parametrizēta P struktūra un iestatīts relatīvi liels Pb. Nākamajā attēlā ir noteikta iestatītā vērtība, kas atrodas turpmākajā darba diapazonā.
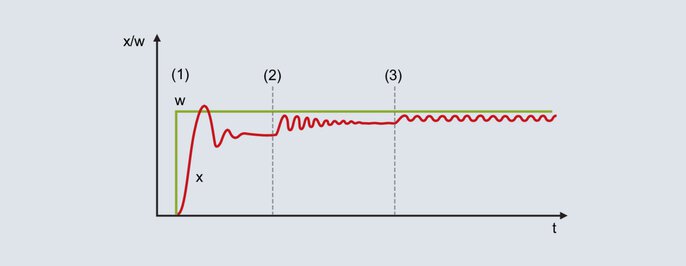
52. attēls: iestatītās vērtības un faktiskās vērtības līkne, izmantojot svārstību metodi
Ja proporcionālā josla ir iestatīta relatīvi liela, faktiskā vērtība pārvietojas uz galīgo vērtību ar nelielu svārstību tendenci [52. attēls (1)]. I struktūras neesamības dēļ pastāv pastāvīga regulēšanas novirze.
Pb tiek samazināts (52. attēls [2]): faktiskā vērtība palielinās un virzās uz galīgo vērtību ar lielāku svārstību tendenci. Noteiktos apstākļos proporcionālā josla tiek samazināta vairākas reizes, līdz faktiskā vērtība pastāvīgi svārstās (52. attēls [3]). Šādai uzvedībai nepieciešamo proporcionālo joslu sauc par Pbc (kritisko Pb), un tā jānosaka pēc iespējas precīzāk (nesamazināt Pb ar pārāk lieliem soļiem).
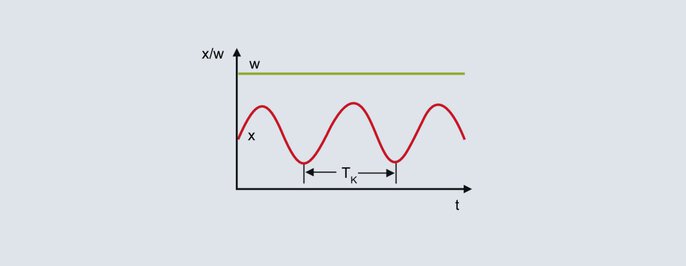
Kritiskais periods
No augšējā attēlā redzamajām faktiskās vērtības nepārtrauktajām svārstībām izriet, ka kritiskā perioda ilgums Tc ir otrais metodi raksturojošais parametrs, kas jānosaka. Kritiskā perioda ilgumu Tc (sekundēs) aprēķina no laika intervāla starp 2 minimālajām vērtībām, piemēram. Lai noteiktu vadības parametrus, Pbc un Tc ievada nākamajā tabulā paredzētajai regulatora struktūrai:
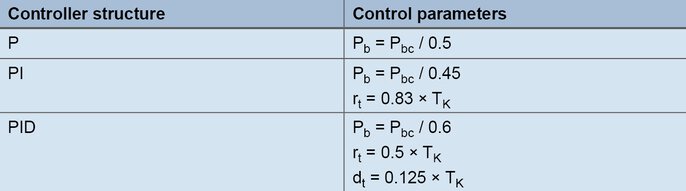
Noteikšanas formulas saskaņā ar svārstību metodi
Metode, pamatojoties uz procesa posma reakciju saskaņā ar Chien, Hrones un Reswick.
Izmantojot šo metodi, vadības parametri tiek aprēķināti salīdzinoši ātri pat lēniem vadības procesiem. Metode ir piemērojama procesiem no otrās kārtas, un tai raksturīgi, ka tajā tiek nošķirtas formulas pārejošai uzvedībai un traucējumu uzvedībai. Vadības procesa pārneses koeficientu, aiztures laiku un kompensācijas laiku aprēķina, pamatojoties uz soļa reakciju.
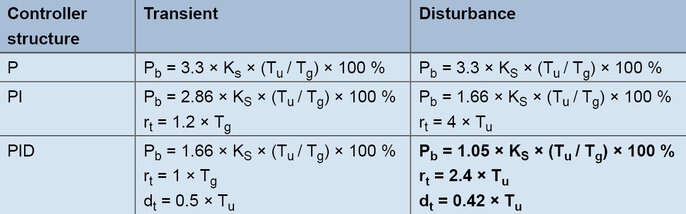
Veidošanas formulas saskaņā ar līnijas soļa reakciju
Piemērs:
Laboratorijas krāsnij jāizmanto regulators ar PID struktūru. Mērķis ir panākt labu traucējumu uzvedību, un tipiskās iestatītās vērtības ir 200 °C. Manuālajā režīmā izejas līmeni pakāpeniski palielina, līdz faktiskā vērtība ir nedaudz zemāka par nākamo iestatīto vērtību (jāgaida attiecīgie kompensācijas procesi). Piemēram, 180 °C temperatūra tiek sasniegta ar 60 % izejas līmeni. Sākot no 60 %, izejas līmeni pēkšņi palielina līdz 80 % un reģistrē faktisko vērtību.
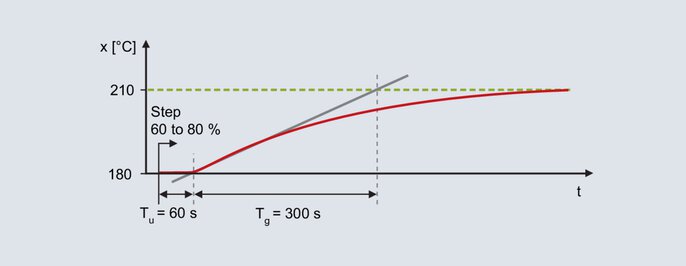
Laboratorijas krāsns pakāpju reakcija
No soļa reakcijas noteikšana notiek ar izliekuma tangentes palīdzību: aiztures laiks Tu = 60 s, kompensācijas laiks Tg = 300 s. Vadības procesa pārraides koeficients izriet no faktiskās vērtības izmaiņas, kas dalīta ar izejas soli.
Equation 22
Izmantojot īkšķa likumsakarības, tiek iegūti šādi traucējumu uzvedības parametri:
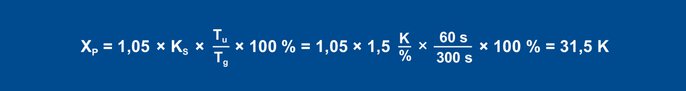
Equation 23
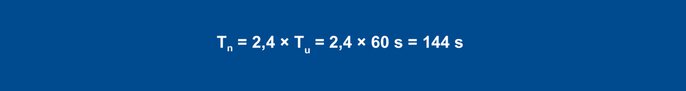
Equation 24
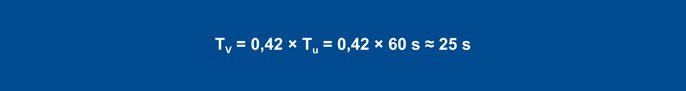
Equation 25
Izvades solis jāveic nākamā darba punkta apgabalā. Turklāt soļa lielumam jābūt pietiekami lielam, lai varētu analizēt faktiskās vērtības gaitu. Kad izejas solis ir noteikts, ir jāgaida faktiskās vērtības beigu vērtība. Alternatīva, kas ietaupa laiku, ir metode pēc pieauguma ātruma.
Metode atkarībā no pieauguma ātruma
Attiecībā uz soļa izmaiņu specifikāciju procedūra ir tāda pati kā metodei, kas balstīta uz procesa soļa reakciju. Pirms soļa maiņas tiek noteikts izejas līmenis, kura rezultātā faktiskā vērtība ir nedaudz mazāka par vēlāk izmantoto iestatīto vērtību.
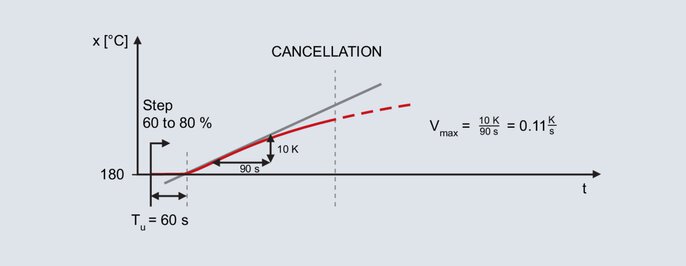
Metodes faktisko vērtību līkne atkarībā no pagrieziena ātruma
Pakāpes maiņa atkal ir norādīta jau minētajai laboratorijas krāsnij, kur nākamais darba punkts arī ir 200 °C. Norādot 60 % izejas līmeni manuālajā režīmā, faktiskā vērtība ir 180 °C. Izejas līmenis pēkšņi tiek palielināts līdz 80 %.
Pēc pakāpju maiņas norādīšanas faktiskā vērtība pēc brīža palielinās. Ierakstīšana turpinās, līdz faktiskā vērtība sasniedz maksimālo slīpumu. Izmantojot šo metodi, tiek zīmēta arī līknes tangente un noteikts aiztures laiks. Otrais raksturojošais parametrs ir maksimālais pieauguma ātrums, kas atbilst infleksijas tangentes slīpumam. Maksimālo pieauguma ātrumu var noteikt, pieliekot slīpuma trīsstūri liektajai tangentei:
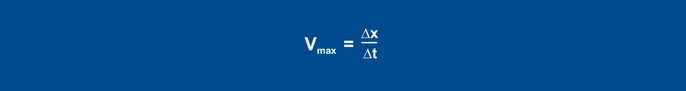
Equation 26
Aprēķinātās vērtības Vmax (0,11 K/s) un Tu (60 s) tiek izmantotas turpmākajās formulās:
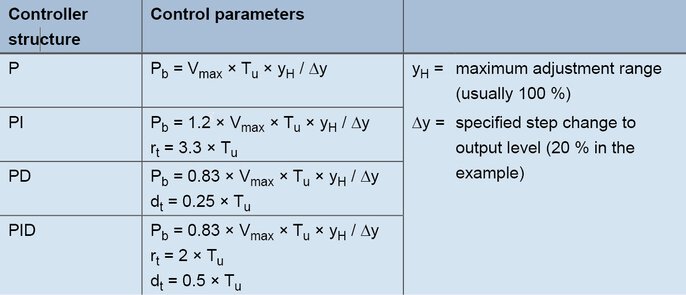
Noteikšanas formulas atkarībā no pieauguma ātruma
PID kontrolierim ar formulām rodas šādas vērtības:
Equation 27
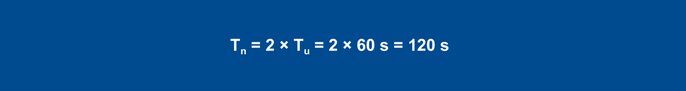
Equation 28
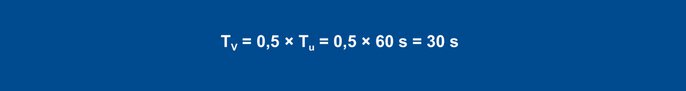
Equation 29
Empīriskā metode kontroles parametru aprēķināšanai
Šo metodi izmanto, lai secīgi aprēķinātu optimālos iestatījumus P, D un I komponentiem. Sākot no sākotnējā stāvokļa (izejas līmenis 0 %), katru reizi tiek noteikta tipiskā iestatījuma vērtība; tāpēc šī metode ir piemērota tikai relatīvi ātriem vadības procesiem (piemēram, ātriem temperatūras vadības procesiem vai vadības mainīgajiem lielumiem, piemēram, ātrumam vai plūsmai).
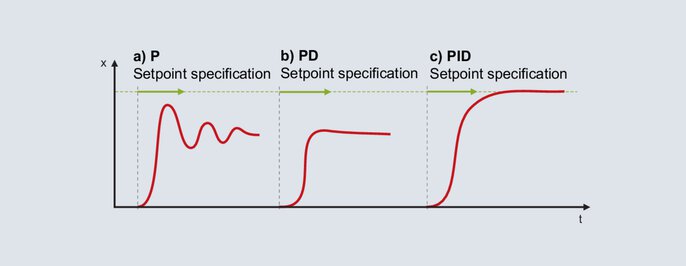
PID regulatora iestatīšana saskaņā ar empīrisko metodi
Vadītājam tiek aktivizēta P struktūra. Tiek iestatīta relatīvi liela proporcionālā josla (izmēri ir atkarīgi no vadības procesa), un tiek norādīta iestatītā vērtība nākamajā darba diapazonā. Faktiskā vērtība lēni virzīsies uz gala vērtību, un tiek radīta relatīvi liela regulēšanas novirze. Pēc tam tiek norādīta iestatītā vērtība ar arvien mazāku proporcionālo joslu Pb. Mērķis ir panākt Pb, ar kuru faktiskā vērtība sasniedz stabilu gala vērtību pēc 2 līdz 3 pilnām svārstībām (56.a attēls). Lai nodrošinātu vienmērīgu palaišanu, struktūra jāpārslēdz no P uz PD. Sākot ar nelielu atvasinājuma laika iestatījumu, iestatīto vērtību nosaka ar arvien lielāku dt. Ja faktiskā vērtība sasniedz galīgo vērtību ar pēc iespējas mazāku svārstību laiku, dt ir optimāli iestatīts (56.b attēls).
Ņemiet vērā: tiklīdz regulators pat tikai vienu reizi palaišanas laikā nosaka izejas līmeni līdz 0 %, tas nozīmē, ka dt ir iestatīts pārāk liels.
I komponente tiek aktivizēta, kad struktūra ir pārslēgta uz PID. Optimālo atiestatīšanas laiku rt parasti nosaka 4 reizes lielāku par iepriekš noteikto dt vērtību. c attēlā parādīta reakcija, ja rt = 4 × dt.
Dažos procesos nav iespējams aktivizēt visus komponentus. Ja, izmantojot P struktūru, ar lielu Pb jau ir radusies nenoregulēta atbildes reakcija, P vai D struktūru nebūs iespējams izmantot. Tā vietā jāizmanto I kontrolieris.
Ja P regulators ir veiksmīgi noregulēts, bet D komponenta ieviešana padara vadības cilpu nestabilu, tiek izmantota PI struktūra.
Piemērojot kādu no šajā nodaļā aprakstītajām regulēšanas metodēm, visticamāk, tiks iegūta stabila, bet ne optimāla vadības reakcija. Vadības rezultātu var vēl vairāk uzlabot, manuāli pārregulējot. Ja PID regulatora reakciju var saskaņot ar kādu no 62b līdz 62e līknēm, šeit atradīsiet informāciju par turpmāko regulēšanu.
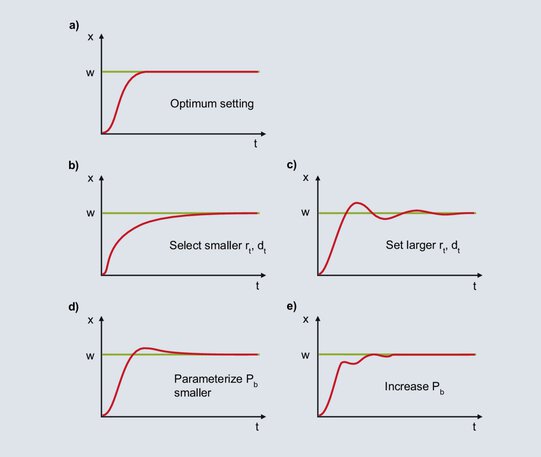
62. attēls: Piezīmes par PID regulatora pēcnoregulēšanu
Diagrammā parādīta PID regulatora optimālā uzvedība.
Pēc iestatītās vērtības noteikšanas faktiskā vērtība strauji pieaug, līdz sasniedz proporcionālo joslu. Ja faktiskā vērtība nonāk proporcionālajā joslā, P komponente tiek samazināta, un I komponente nodrošina vērtības pielāgošanu iestatītajai vērtībai. I komponentes palielināšanās notiek lēni relatīvi lielā rt dēļ, un vadības novirze tiek lēnām novērsta. Ātrākai integrācijai rt ir jānosaka mazāks; arī dt tiek samazināts atbilstoši attiecībai dt/rt = 1/4.
Kad faktiskā vērtība nonāk proporcionālajā diapazonā, I komponente palielina izejas līmeni. Palielinājums turpinās, līdz faktiskā vērtība sasniedz iestatīto vērtību. Parādītajā piemērā I komponente veido pārmērīgu izejas līmeni, līdz tiek novērsta regulēšanas novirze un faktiskā vērtība pārsniedz iestatīto vērtību. Ja ir negatīva vadības novirze, izejas līmenis tiek samazināts pārāk ātri, un faktiskā vērtība nokrīt zem iestatītās vērtības, un tā tālāk. Faktiskās vērtības simetriskas svārstības ap iestatīto vērtību liecina par pārāk mazu rt. rt ir jāpalielina un arī dt jāpalielina atbilstoši attiecībai dt / rt = 1/4.
I komponente veidojas no brīža, kad faktiskā vērtība nonāk proporcionālajā joslā, līdz regulēšanas novirzes novēršanai. Lielā Pb dēļ I komponente sāk veidot savu izejas līmeni jau tad, kad ir liela regulēšanas novirze. Sakarā ar lielo vadības novirzi sākumā I komponente relatīvi ātri veido savu izejas līmeni. Kad vadības novirze tiek novērsta, I komponente ir pārāk liela, un faktiskā vērtība pārsniedz iestatīto vērtību. Ar mazāku Pb iestatījumu, ja ir mazāka regulēšanas novirze, I komponente sāk veidot savu izejas līmeni attiecīgi lēnāk. Attēlotais vienreizējais pārsniegums kļūst mazāk iespējams.
Ja Pb ir iestatīts pārāk mazs, P komponentes izejas līmenis samazinās īsi pirms iestatītās vērtības sasniegšanas. Kad faktiskā vērtība nonāk proporcionālajā diapazonā, P komponente strauji samazinās un faktiskā vērtība samazinās. Lielākas regulēšanas novirzes dēļ izejas līmenis kļūst lielāks un faktiskā vērtība palielinās. Proporcionālajā joslā nelielas faktiskās vērtības izmaiņas izraisa lielas izejas līmeņa izmaiņas, kā rezultātā rodas liela svārstību tendence. To nomierina, palielinot proporcionālo joslu.
